Nächste Seite: Re: Jetzt neu Uebung Aufwärts: Graphen, Schaltwerke und Zahlen Vorherige Seite: Re: Jetzt neu Uebung
Ich denke, ich weiss dann auch was Hamilton. Graf ist sozusagen klassischer Kreis ist genauso wie in Pentagramm Hamilton, Graf, weil Hamilton Graf ist ein Grafen Euler Graf, bei dem Jaeger der Knoten genau einmal durchlaufen wird. Wie muss man das verstehen. ein Euler Graf ist ja zum Beispiel. Mit Knoten versehen, bei denen die valenz jeweils gerade ist das notwendig, weil wenn ich zweimal in Knoten reingehe und nur einmal rausgehe, dann gehe ich die Kante mehrfach. Trotzdem ist ja die valenz gerade ist nicht garantiert, dass ich ein Knoten nicht zweimal durch laufe. Graf ist genau dann auch ein Hamilton Kreis wenn der Knoten nur einmal durchlaufen wird d.h. zum Beispiel zwei Kanten hat das hab ich jetzt so in Erfahrung gebracht ueber den Hamilton, Graf. Ich werde mich damit auch noch genauer beschaeftigen.
Ach so, ich hab das chinesische Brieftraeger Problem verstanden abgesehen davon, dass man den Algorithmus von Danzig und dijkstra verwenden kann, aber offensichtlich nicht muss. Abgesehen davon ist es chinesische Brieftraeger Problem jedenfalls auf jeden Fall geloest, wenn es den Euler Graf ist und es bedeutet, jeder Weg ist der richtige Weg. Also jeder optimale Weg, der den Eulergraphen erfuellt ist, der richtige Weg stellt sich die Frage, warum der Euler Graf laeuft natuerlich kein Weg doppelt. Jetzt gibt es zwischen Punkt A und Punkt B. Eine Verbindung zwischen Punkt B und Punkt C. Eine Verbindung und zwischen Punkt A und C eine Verbindung gut jetzt koennte man sagen ich bin kein Weg doppelt gegangen stellt sich trotzdem die Frage zwischen den wegen besteht ja sozusagen eine Laenge. Na ich hab das wahrscheinlich ganz falsch beantwortet. Ich habe so argumentiert, dass zwischen den wegen eine Laenge besteht und und das zweites Eulersche Problem geloest waere. Sozusagen warum allerdings waere damit die Laenge die kuerzeste. Ich hab so argumentiert. Ich koennte ja sowohl den Einweg gehen als auch den anderen vom auf dem Papier vom Satz des Pythagoras zum Beispiel was die Addition der Laengen in der Geometrie betrifft, wuerde sich die Gesamtheit ausgleichen so hab ich argumentiert. Jetzt sehe ich auf einmal, dass die Argumentation totaler Unsinn ist sozusagenweil ich gehe ja den Eulergrafen und damit gehe ich jeden Weg einmal das chinesische Brieftraeger Problem bedeutet ja wir sind sozusagen bei der Post und ich hab auch so gedacht naja ich muss ja jeden Platz einmal ablaufen. Sozusagen in Wirklichkeit bin ich ja bei der Post und es genuegt nicht, dass ich jeden Platz einmal ablaufe, weil die Kanten sind ja die Strassen und in den Strassen sind die Empfaenger der Briefe. Die Nutzer der Post und die wollen allen Brief d.h. ich muss sowieso jede Strasse einmal gehen aus der Sicht der Post d.h. ich muss jeden Weg einmal gehen und die Argumentation ist hinfaellig. Ich hab wie gesagt so argumentiert. Naja, das ist ein Euler Graf und wenn ich jeden Weg einmal gehe, es gibt ja kuerzere und laengere Wege am Ende gleicht sich das geometrisch vom Satz des Pythagoras aus, zum Beispiel vom Satz des Pythagoras sei nicht durch den aber von der Gesamtheit durch die Geometrie auf dem Papier kombiniert mit dem Euler Graf wuerde sich das sozusagen ausgleichen, so hab ich gedacht, dabei bin ich davon ausgegangen mehr oder weniger intuitiv, dass ich gewisse Wege ja nicht gehe. Ich habe sozusagen alle Knoten erreicht, aber das ist ja nicht das Problem. Der Postbote muss ja jedes Haus einmal besuchen d.h. jeden Weg einmal geben. Insofern ist es logisch, dass das Problem geloest ist, solange es ein Euler Graf ist und solange ich das als Euler Problem behandelt d.h. jeden Weg einmal geh ist das Problem geloest es ist ja letztenendes hier. Nur ne Frage der Reihenfolge gehe ich erst die Strasse zwischen A und B oder die Strasse zwischen A und C. Hier muss ich die Strassen ja nur addieren. Ich muss die Strassen addieren und von der Summe, in dem ich die Strassen addiere, ist es vollkommen belanglos, in welcher Reihenfolge ich die Strassen gehe, die Summe der Strasse bleibt und damit ist das Problem auch geloest. Die Summe der Strasse bleibt und es ist kein geometrisches Problem. Ich bin irgendwie davon ausgegangen naja eine gewisse Kante werde ich ja nicht gehen, aber ich muss ja jede Kante gehen. Der Brieftraeger muss ja jedes Haus erreichen und wenn ich nicht jede Kante gehen wuerde, dann koennte es ja sein, dass ich das Problem trotzdem Euler schloesse. da hab ich falsch gedacht. Das entspricht ja dann nicht mit dem Eulergrafen und sich dann auf dem Papier sozusagen bewiesen. Massen koennte man jetzt sagen ausgleichen wuerde dieses geometrische wuerde von der Laenge sozusagen wieder wieder die selbe Laenge ergeben. Aber das ist ja Unsinn weil ich muss ja jede Kante einmal gehen und wenn's Neuler Graph ist, dann ist es geschehen.
Die Frage ist, was ist wenn das keine Eulergraph ist wenn also gewisse Knotenpunkte also gewisse Plaetze, wo sich die Strassen kreuzen keine gerader Anzahl an Kanten haben die rein und rausgehen und jetzt kommt dieses Problem von Djkstra und Danzig und das muss man jetzt scheinbar nicht verstehen das kann man zur Loesung benutzen. Die Antwort ist einfach ich addiere den kuerzestem Weg. Ich muss jetzt einen Weg doppelt gehen. Ich muss irgendeinen Weg doppelt gehen und die Frage stellt sich jetzt welchen Weg geh ich doppelt. Die Antwort ist ganz einfach. Ich suche den kuerzestem Weg, den es noch gibt. Wenn es kein Euler Graf ist d.h. die Anzahl der Kanten, die rein und raus wird. Aus einem Knoten ist garantiert, dass ich einen Weg doppelt gehen muss. Welchen Weg muss ich denn jetzt doppelt gehen? Das ist ganz einfach. Ich suche den kuerzestem Weg. Das ist ja eine Menge der Wege das ist die Menge der Kanten suche ich den kuerzestem Weg und wenn ich den habedann nehme ich diesen Weg zweimal also unter der Menge der Kanten unter der Menge der Wege und dann ist mein Problem erfuellt aber da ist der kuerzeste Weg ist hab ich die Kuerz moeglichste Distanz zurueckgelegt
Ich probiere das mit Google Maps gleich mal aus. Ich habe ja bisher beschlossen auf Google Maps die Sache mal auszuprobieren allerdings mit dem Eulergrafen und ich werde das Problem jetzt nicht haben weil ich kenne ja das Chinese Postboten ble. Das bedeutet einfach ich muss noch den kuerzestem Weg suchen und den dazu addieren, weil ich den doppelt gehen muss. Jetzt kann ich das mal mit Google ausprobieren. Ich nehme gewisse Plaetze und gewisse Strassen in Tuebingen. Der Unterschied besteht darin mit Google. Ich kann ja zwei Orte eingeben d.h. zwei Plaetze und jetzt kann ich die Differenz zwischen den zwei Plaetzen ausrechnen so jetzt kann ich das einerseits in der Realitaet mal ablaufen und den die die Karte mitlaufen lassen von dem Smartphone auf der einen Seite auf deiner Seite. Ich kann ja in Google zwei Plaetze eingeben und dann kann ich die Differenz die Weglaenge von Google ausrechnen lassen. Google gib mir ja die entsprechende Weglaenge an, wenn ich zwei Plaetze eingebe, wie lange ich laufen muss. Insofern suche ich mir jetzt gewisse Plaetze in Tuebingen auf Google Maps raus. Ich stelle selber einen Eulergrafen. Da wo es keine Eulergrafen ist, mache ich mit dem kuerzestem Weg ein draus und wenn ich das habe, dann gebe ich jeden Platz ein jeden einzelnen Platz. Berechne die Differenzen der Wege und ich kann ja verschiedene Eulergrafen in verschiedene Eulertouren. In dem Eulergrafen gibt es verschiedene Eulertouren. Das ist ein Euler Graf aber da gibt es verschiedene Eulertouren und ich kann jetzt verschiedene Eulertouren errechnen, indem ich einfach verschiedene Eulertouren gehe und in dem ich das gemacht habe, kann ich die Laenge der Wege addieren und da dieses chinesische Postboten Problem geloest ist, muesste trotz allem jedes Mal dieselbe Differenz dieselbe Wegstrecke herauskommen
Also, man sieht jetzt hier, google maps, und im gegensatz zu den grossen Plaetzen von Tuebingen, ich sage gleich, das macht sicher spass, das mal in der Realitaet auf der Strasse aus zu probieren, sind hier einfache Strassenkreuzungen, die keinen Namen tragen. Das ist etwas schwierig, Google Maps, ab zu fragen, wenn die Kreuzung keinen Namen hat, der Abstand zwischen den Kreuzungen, also den Knoten.
Umgekehrt, dann wuerde ich jede Kreuzung markieren, mit einem Blauen, roten oder wie auch immer Punkt und haette meine Knoten
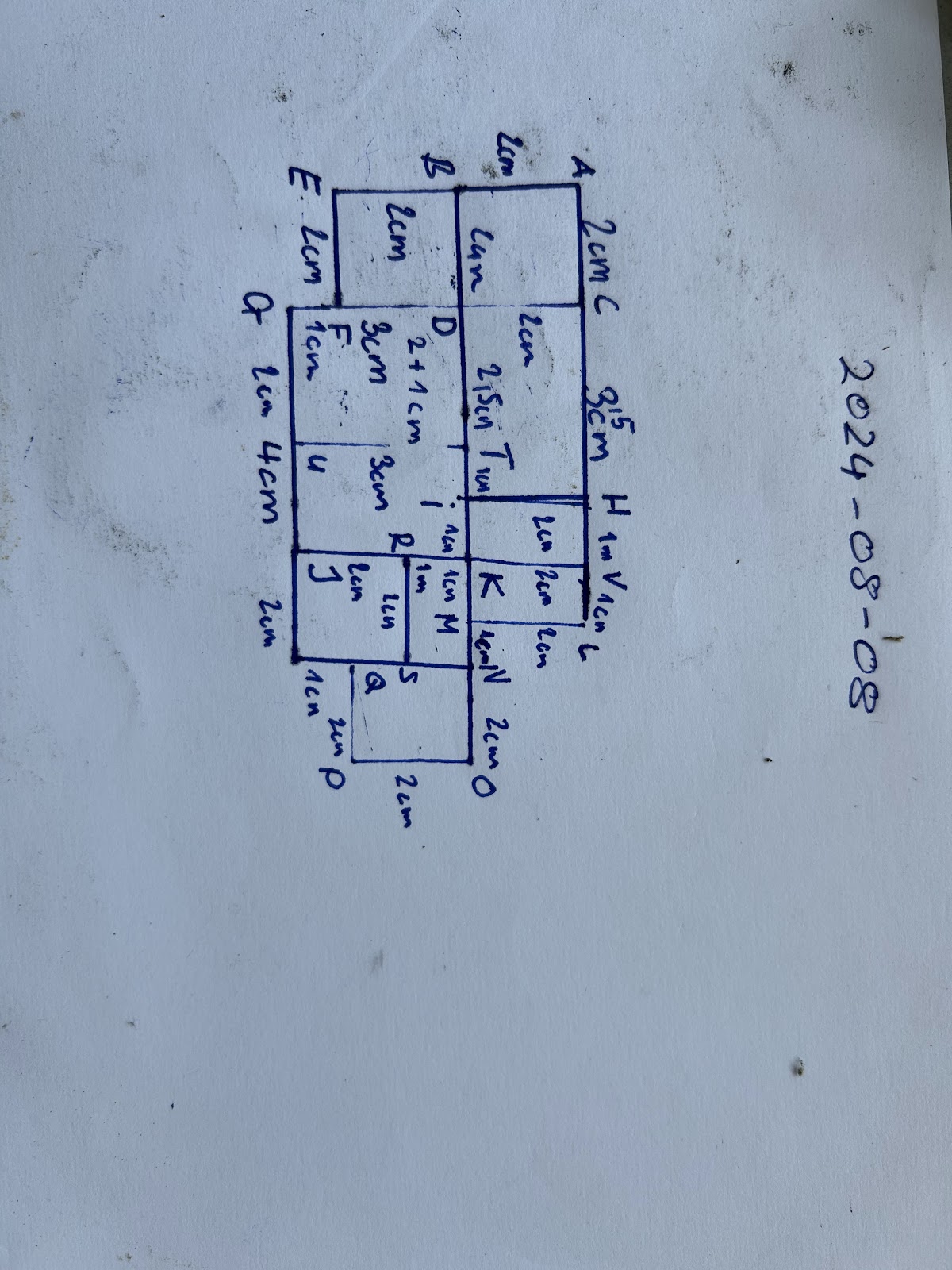
Umgekehrt, ich kann das Chinesische Postbotenproblem ganz anders testen, mal in der Realitaet, das ist richtig. Aber ich kann ja auch einfach mal ein Papier nehmen, sie wissen der Satz des Pythagoras, funktioniert auch mit Seiten a und b, mit 2cm und 3cm, da geht der genauso gut und ich kann auf das Papier ein relativ, senk und wagerechtes Netz an Strassen zeichnen, was Strecken mit dem Fuellfederhalter bedeutet, die etwa 2cm oder 4cm, aber genaue integre laengen haben, dann kann ich das auf dem Papier ausprobieren
Ich habe ja meine Homepage und da kann ich dieses Experiment, auch guten gewissens Posten, der Unterschied ist, dass ich die Kreuzungen ruhig a und b nennen kann, aber die Distanzen kenne. Ich poste das gleichzeitig auf Facebook, hier besteht natuerlich in letzter Zeit das Problem, wenn ich meine eigenen Aufschriebe poste, oder was auch immer, gemacht mit dem Fuellfederhalter, dann glaubt Facebook das haette ich nicht selber gemacht
Tschuldigung, ich hab gewohnheitsmaessig falsches Datum dran geschrieben das heisst zehnter heute ist der 10. August weiss ich auch. Heute hat meine Mutter Geburtstag