T1cmrmn
Jetzt mache ich vollstaendige Induktionsaufgaben
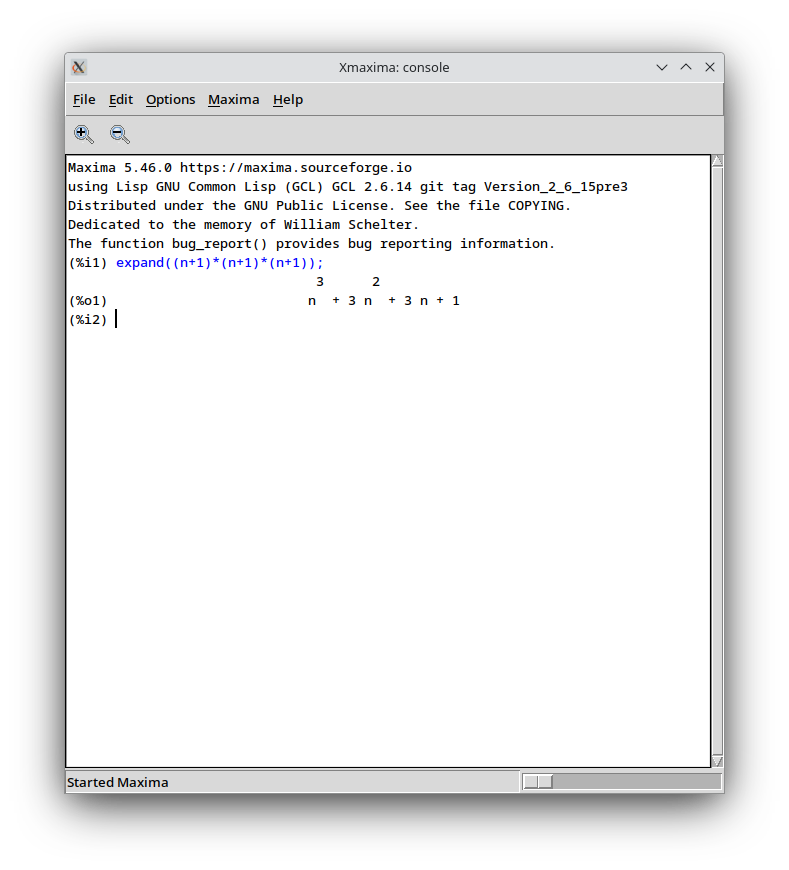
xmaxima sagt dasselbe
Kann man mit dem Binomialkoeffizient wie bei Polynomen zeigen
Ich glaube schon
erstens
Binomialkoeffizient
fuer 3 gilt, das ist das oberste
Was ist nicht erstaunlich hier ist kein Faktor
Jetzt nachgucken, ich habe noch nicht geguckt. Oder ich rechne mit Hand nach.